Key Ideas
- Developed a clever maze navigation task consisted with multiple obstacles to understand how humans form task construals in their brain
Theoretical details
Task construals
Let a task \(\mathcal{T}\) is consisted with state space \(\mathcal{S}\), action space \(\mathcal{A}\), transition function \(\mathcal{P}: \mathcal{S} \times \mathcal{A} \times \mathcal{S} \rightarrow [0, 1]\), and a utility function \(\mathcal{U}: \mathcal{S} \rightarrow \mathbb{R}\). Let plan \(\pi: \mathcal{S} \times \mathcal{A} \rightarrow[0, 1]\), then the value function of following certatin plan will be:
\[V_{\pi}(s)= U(s) + \sum_{a \in \mathcal{A}} \pi(a| s) \sum_{s' \in \mathcal{S}} P(s'|s, a) V_{\pi}(s')\]Therefore, standard planning algorithms optimize value directly planning over a fixed task representation. Humans however might constructed a simplified version of the task, and use this simplified version in planning.
Let us say the agent has \(N\) primitive cave-effect relationships. Then,
\[\phi_i : \mathcal{S} \times \mathcal{A} \times \mathcal{S} \rightarrow [0, 1], \,\,\,i=1, \cdots , N\]where each \(\phi_i(s'\mid s, a)\) is a potential function representing local effect of a given action \(a\) in a given state \(s\). The task construal \(\mathcal{T}_c\) can be produced with \(c \subseteq \{ \phi_1, \cdots, \phi_N \}\), and the transition probability can be expressed as:
\[P_c(s' | s, a) \propto \prod_{\phi_i \in c} \phi_i (s' \mid s, a)\]Ideally, the task construal \(\mathcal{T}_c\) and the original task \(\mathcal{T}\) would share the same state space, action space and utility function, but the construed transition function may be simpler than the actual task.
The expected utility starting at state \(s_0\) when following \(\pi_c\), which is the plan optimized based on the task construal \(\mathcal{T}_c\) would be:
\[U(\pi_c ) = U(s_0) + \sum_{a} \pi_c (a \mid s_0) \sum_{s'} P(s' \mid s_0, a) V_{\pi_c}(s')\]Note that the transition probability used in the calculation is the actual transition dynamics \(P\), not \(P_c\).
The utility function \(U(\pi_c)\) would reach it’s optimal value as the task construal gets closer to the actual task. However, this requires more cognitive capacity as it’s complexity gets higher. The value of representation (VOR) therefore can be defined as below:
\[VOR(c) = U(\pi_c) - C(c)\]where \(C(c) = \lvert c\rvert\), and \(\lvert c\rvert\) is the cardinality of \(c\).
Assuming that participants select construal accordint to the softmax decision rule, the probability to choose construal \(c\) would be:
\[P(c) \propto \text{exp} \left[ \alpha^{-1} VOR(c) \right]\]where \(\alpha>0\) is a temperature parameter. Then, the expected awareness of a specific obstacle \(i\) would be:
\[P(\text{obstacle}_i) = \sum_c \mathbb{1} \left[ \phi_{\text{obstacle}_i} \in c \right] P(c)\]Results
People are more aware of obstacles which are crucial in planning
As presented on the below figure, participants were shown a maze composed of a starting location, a goal location. The maze was different for each trial, while the center plus symbol (+) black walls always appeared.
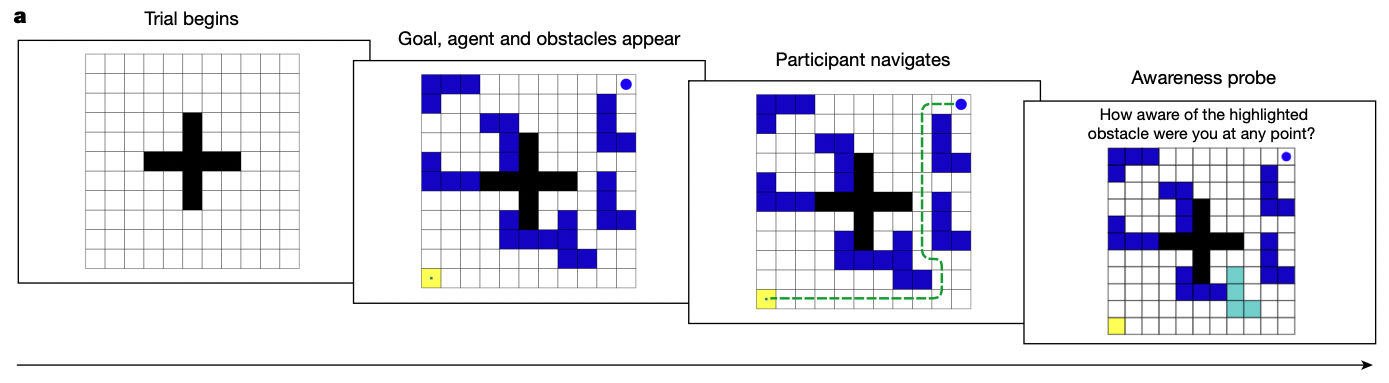
Note that the maze is fully observable, and the structure of the maze emerges by composition of idividual obstacles. However, since not all obstacles are necessary in deciding the shortest path to the goal, participants need to decise which obstacles to integrate in the representation for planning.
By simply asking whether the participants were aware of a chosen obstacle, we can check whether that specific obstacle was integrated in one’s construal representation: if it was included, there will be a higher chance to be self-aware of it after playing the navigation task.
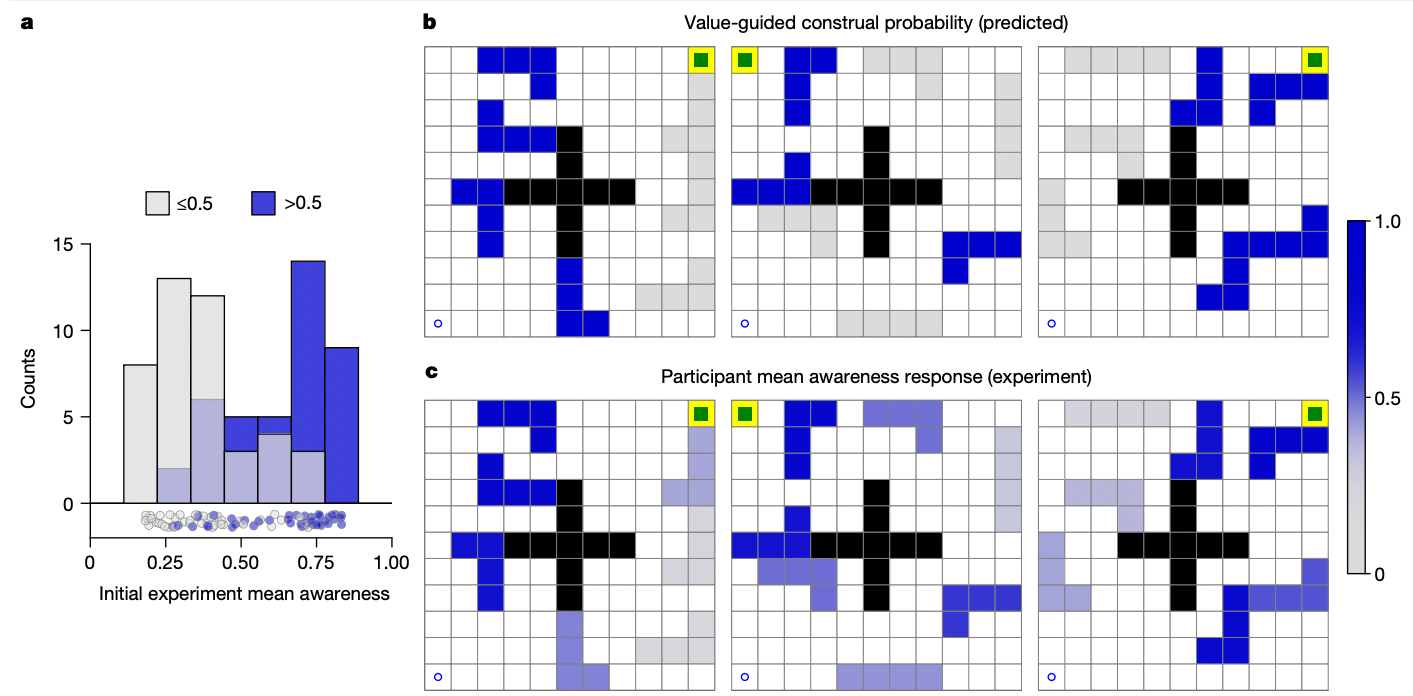
The obstacles were divided into two groups based on the predicted awarness of each obstacle. Obstacle blocks with high expectation of being awared had significantly higher mean awarness, compared to blocks with low expectation. However, strictly speaking, measuring the awareness a step away from accessing the direct memory.
People memorize obstacles crucial in planning, while neglecting others
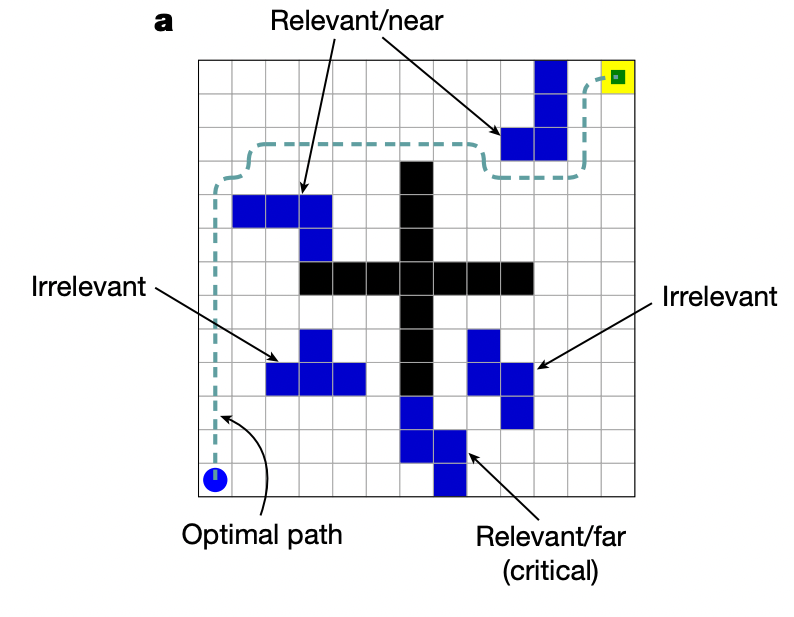
If the obstacle is integrated into the task contrusal of the participant, they will be able to recall the location of the obstacle. In the next experiment, a maze was given with three different types of obstacles: 1) relevant obstacles placed near by the optimal trajectory, 2) relevant obstacles placed remote to the optimal trajectory, 3) irrelevant obstacles.
While playing the navigation task, this time the obstacles turn invisible (but still exists). After the navigation task, participants were asked, “An obstacle was either in the yllow or green location (but not both), which one was it?” and could select either option. After the selection, participants answered their confidence of their own choice.
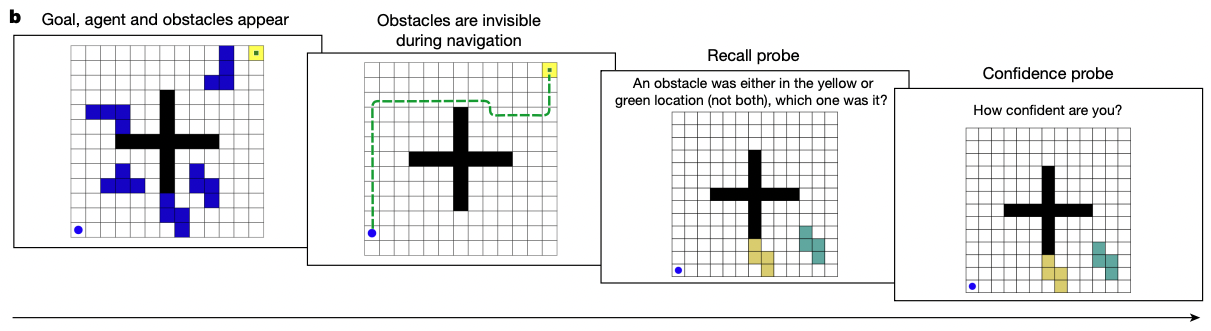
As a control task, participants responsed to the recall probe 1) after watching a maze-like stimuli but not playing it (perception control), or 2) after simply following ‘breadcrumbs’ through the aze (execution control)
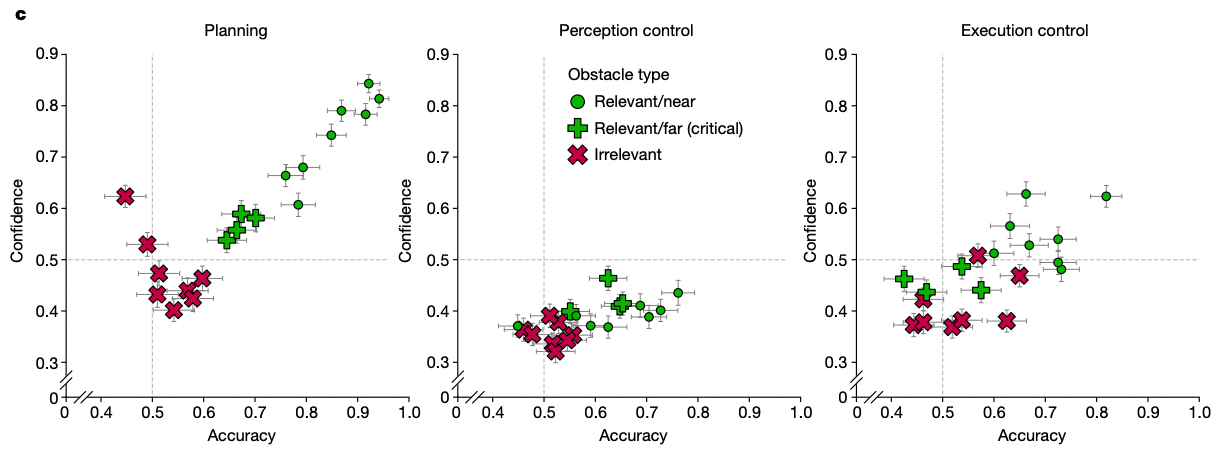
As we can confirm in the above figure, participants had significantly higher accruacy in recalling relevant obstacles for both near and far cases, while having accuracy near chance level for irrelevant obstacles. This tendency diminished in both perception control and execution control sessions. Hence, we can conclude that people integrate into contrusal and memorize obstacles that are crucial in decision making, while neglecting obstacles that aren’t.
Food for thought
- People might have varying balance tendency between complexity and utility. Can we predict the balance point (or at least preference between high utility and low complexity) in an individual level?
- (I know that I always come up with this but) What would be the biological entity of VOR?
- How can we relate this work with successor representation?