Key Ideas
- Learns long-horizon behaviors from images purely by latent imagination; predicts both actions and state values in the latent space.
Theoretical details
Formulating Task
Let us formulate visual control as a POMDP with the discrete-time step \(t \in [1; T]\), continuous vector-valued actions \(a_t \sim p(a_t|o_{\leq t}, a_{<t})\) generated by the agent, and high-dimensional observations and scalar rewards \(o_t, r_t \sim p(o_t, r_t | o_{<t}, a_{<t})\). The goal is to develop an agent that maximizes the expected sum of rewards \(\mathbb{E}_{p}(\sum^T_{t=1}r_t)\). 
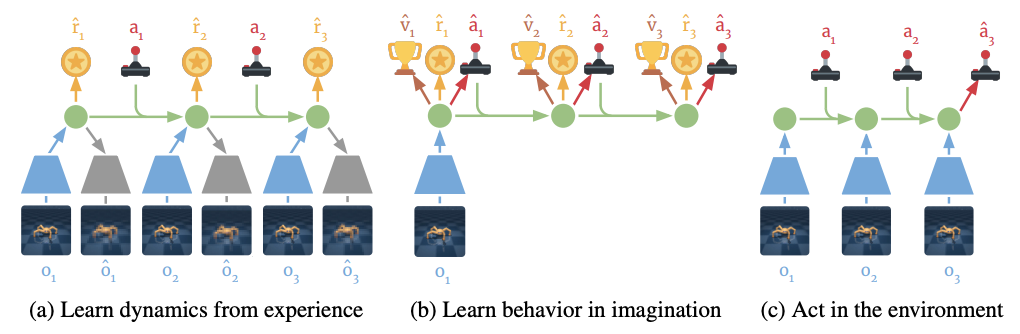
Latent dynamics
Dreamer uses a latent dynamics model that consists of three components: 1) Representation model, 2) Transition model, and 3) Reward model:
\[\text{Representation model: } p( s_t | s_{t-1}, a_{t-1}, o_t)\] \[\text{Transition model: } q(s_t |s_{t-1}, a_{t-1})\] \[\text{Reward model: } q(r_t |s_t)\]Here, \(p\) is used for distributions that generate samples in the real environment, while \(q\) is used for their approximations that enable latent imagination. The great strength of this approach is that it directly learns the transition dynamics in latent space, resulting in a low memory footprint and fast predictions of thousands of imagined trajectories in parallel. Another strength of learning state dynamics in latent space directly is that by preventing prediction of the observation itself spanned in high-dimensional space, the task to learn transition dynamics becomes something more capable to be learned. Imagined trajectories start at the true model state \(s_t\) of observation sequences drawn from the agent’s past experience. By using the models we mentioned above, predictions of \(s_{\tau}\), \(r_{\tau}\) and \(a_{\tau}\) are made, while the objective of this prediction is to maximize the expected imagined rewards: \(\mathbb{E}_{q} \left(\sum_{\tau=t} ^\infty \gamma^{\tau-t} r_{\tau} \right)\)
To describe latent dynamics with a world model, the paper first uses an approach suggested in PlaNet. This approach consists of four following components:
\[\text{Representation model: } p_{\theta}(s_t | s_{t-1}, a_{t-1}, o_t)\] \[\text{Observation model: } q_{\theta}(o_t | s_t)\] \[\text{Transition model: } q_{\theta}(s_t |s_{t-1}, a_{t-1})\] \[\text{Reward model: } q_{\theta}(r_t |s_t)\]We assume latent dynamics in the latent space to be a Markov decision process that is fully observed. Components are optimized jointly to maximize variational lower bound (ELBO):
\[\mathcal{J}_{\text{REC}} \doteq \mathbb{E}_{p}\left( \sum_t \left( \mathcal{J}^t_O + \mathcal{J}^t_R + \mathcal{J}^t_D \right) \right)\]where
\[\mathcal{J}_O^t \doteq \text{ln }q(o_t | s_t), \, \, \mathcal{J}_R^t \doteq \text{ln }q(r_t | s_t)\] \[\mathcal{J}_D^t \doteq -\beta \text{ KL} \left(p(s_t | s_{t-1}, a_{t-1}, o_t) \| q(s_t | s_{t-1}, a_{t-1}) \right)\]Since predicting the pixel-based high-dimensional observation \(o_t\) from \(s_t\) requires high model capacity, we can instead encourage the model to increase mutual information between states and observations. This will replace the observation model with a state model:
\[\text{State model: }q_{\theta}(s_t | o_t)\]Then, using Bayes rule and InfoNCE mini-batch bound, we can redefine the objective function as:
\[\mathcal{J}_{\text{NCE}} \doteq \mathbb{E}_{p}\left( \sum_t \left( \mathcal{J}^t_S + \mathcal{J}^t_R + \mathcal{J}^t_D \right) \right)\]where
\[\mathcal{J}^t_S \doteq \text{ln }q(s_t | o_t) - \text{ln } \left( \sum_{o'}q(s_t|o') \right)\]Action and value models
The dreamer uses an actor-critic approach, consisting of an action model and a value model. The action model implements the policy and aims to predict actions that solve the imagination environment, while the value model estimated the expected imagined rewards that the action model achieves from each state \(s_{\tau}\). Let’s consider an imagined trajectory with a finite horizon \(H\). Then:
\[\text{Action model: }a_{\tau} \sim q_{\phi}(a_{\tau} | s_{\tau})\] \[\text{Value model: } v_{\psi}(s_{\tau}) \approx \mathbb{E}_{q(\cdot | s_{\tau})} \left( \sum_{\tau=t} ^{t+H} \gamma^{\tau-t} r_t \right)\]Both models are trained with a typical policy iteration fashion. To enable the action model to learn the policy itself for a given state \(s\), the paper uses reparameterized sampling: \(a_{\tau} = \text{tanh } (\mu_{\phi} (s_{\tau})+\sigma_{\phi} (s_\tau)\epsilon), \, \, \,\epsilon \sim N(0, \mathbb{I})\)
State values can be estimated in multiple ways that trade-off bias and variance:
\[V_R (s_{\tau}) \doteq \mathbb{E}_{q_{\theta}, q_{\phi}} \left( \sum_{n=\tau} ^{t+H} r_n \right)\] \[V_{N}^k (s_{\tau}) \doteq \mathbb{E}_{q_{\theta}, q_{\phi}} \left( \sum_{n=\tau} ^{h-1} \gamma^{n-\tau}r_n + \gamma^{h-\tau} v_{\psi} (s_h) \right), \,\,\,\, \text{with } h=\text{min }(\tau+k, t+H)\] \[V_{\lambda}(s_{\tau}) \doteq (1-\lambda) \sum_{n=1}^{H-1} \lambda^{n-1} V_N^n(s_\tau) + \lambda ^{H-1}V_N^H(s_{\tau})\]\(V_R\) simply sums the rewards from the imagination trajectory until it reaches the horizon, and ignores rewards beyond it. It, therefore, makes action models learn without a value model. \(V^k_N\) on the other hand, estimates rewards beyond \(k\) steps with the learned value model. Finally, \(V_{\lambda}\) is an exponentially weighted average of \(V_N^k\) for different \(k\), in which to balance between bias and variance. Here, the dreamer uses \(V_{\lambda}\) to estimate the value function. To update the action and value models, \(V_\lambda (s_{\tau})\) is estimated for all states \(s_{\tau}\) along the imagined trajectories. The objective of the value model \(v_\psi(s_\tau)\) is to regress the value estimates. Thus, the learning objective would be: \(\text{min}_{\psi} \mathbb{E}_{q_{\theta}, q_{\phi}} \left( \sum_{\tau=t} ^{t+H} \frac{1}{2} \left\| v_{\psi} (s_\tau) - V_{\lambda}(s_\tau) \right\|^2 \right)\)
Likewise, the objective for the action model \(q_{\phi}(a_{\tau}\mid s_{\tau})\) is to predict actions that result in state trajectories with high-value estimates. We can formulate this as:
\[\text{max}_{\phi} \mathbb{E}_{q_{\theta}, q_{\phi}}\left( \sum_{\tau=t}^{t+H} V_{\lambda}(s_\tau) \right)\]To sum up, the whole scheme of Dreamer algorithm is as below:
Results
Performance between different value estimations
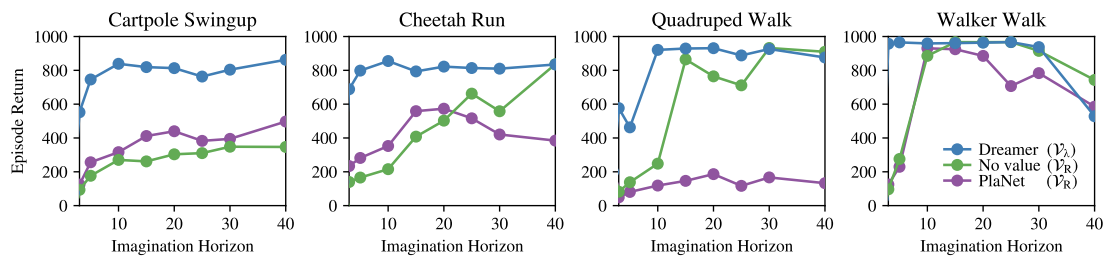Remind that both PlaNet and No value case uses only directly sampled rewards (\(\mathcal{V}_R\)), while Dreamer uses estimated value function to estimate rewards (\(\mathcal{V}_{\lambda}\)). Here, we can see several interesting findings:
- Dreamer shows more robust results, against the different lengths of imagination horizons.
- Dreamer performs quite well even for short horizons.
- Except for the cart pole swing-up task, no value case can reach the performance of Dreamer if the imagination horizon is long enough.
- No value case outperforms PlaNet, even though they both do not learn the value function
Performance comparison to existing methods
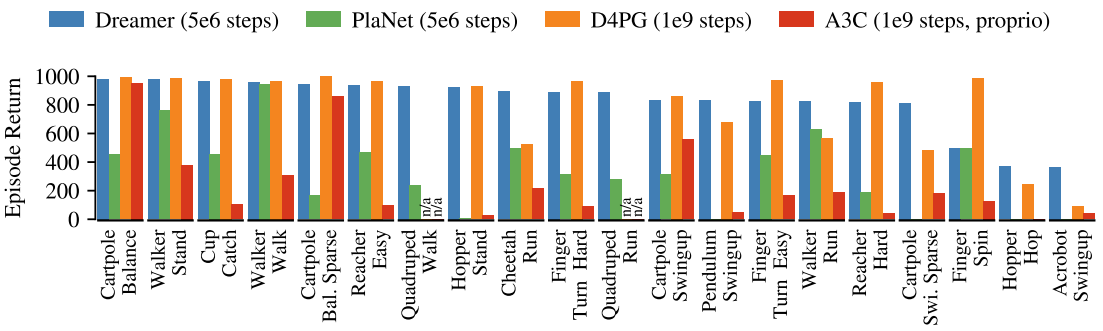
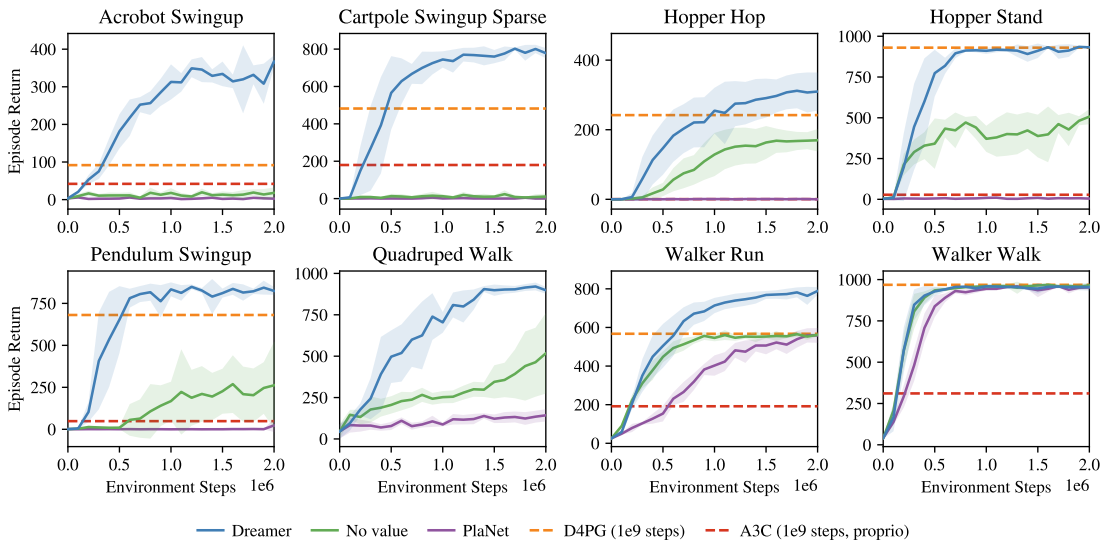
- Dreamer inherits data efficiency of PlaNet while exceeding the performance of the best model-free agents. (D4PG, A3C) This means learning behaviors by latent imagination can outperform methods based on experience replay.
Food for thought
- Why does no value case still outperform PlaNet?
- Can dreamer handle more complicated observation space with more variance? If not, what would be other alternative ideas to overcome this problem?
Reference
[1] Hafner, D., Lillicrap, T., Ba, J., & Norouzi, M. (2019). Dream to control: Learning behaviors by latent imagination. In International Conference on Learning Representations (ICLR) 2020
[2] Hafner, D., Lillicrap, T., Fischer, I., Villegas, R., Ha, D., Lee, H., & Davidson, J. (2019). Learning latent dynamics for planning from pixels. In International Conference on Machine Learning (ICML) 2019
[3] Poole, B., Ozair, S., Van Den Oord, A., Alemi, A., & Tucker, G. (2019, May). On variational bounds of mutual information. In International Conference on Machine Learning (ICML) 2019